拍照取角最大问题报告

尊敬的老师：

在寒假期间，本小组进行了课题为“拍照取角最大问题”的研究，现就课题完成情况作出如下报告：

一、 背景：

数学是一门基础学科，学习数学可以培养我们思维的严谨性，对其他学科的学习有所帮助。使我们遇到问题能够冷静思考，并提高探究能力。

最优化概念反映了人类实践活动中十分普遍的现象，即要在尽可能节省人力、物力和时间前提下，争取获得在可能范围内的最佳效果，因此，最优化问题成为现代数学的一个重要课题，涉及统筹、线性规划一排序不等式等内容。通俗的讲，就是如何使得一件事情做到最好的问题。

拍照取角问题在生活中十分常见，在此问题上寻求最优化结论，由此得出本次课题研究的主要内容：

在公路的一侧从A至B有一排楼房，想在公路I上的任何一处拍一张正面照，任何选择公路上的点，使拍摄的一排楼房的取景最大（点A与点B与直线I的各种位置关系讨论）

二、过程

第一次活动（2024年2月1日）：

1.在地图上寻找与课题类似情景地点

2.实地探查，携带照相机等类似拍照设备，拍照模拟

3.大致寻找拍照时取角最大的位置

4.测量所得地点的位置，记录

5.多次寻找，尽可能寻找更准确的结果

第二次活动（2024年2月6日）

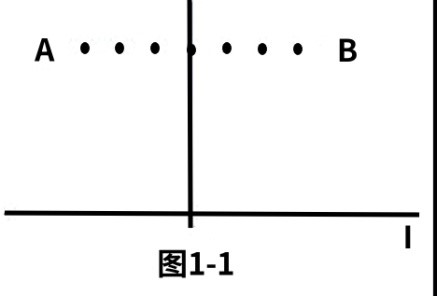
1. 分析：用数学的语言来说就是已知同一平面上两点及一直线，（两点代表一排楼房的两端，一直线代表公路），两点在直线的同侧，在已知直线上求一点C，使AC与BC的夹角角ABC最大。（见图1-1）

2. 建模：两点在I的同侧，但其位置可能出现三种情形

（1）两点的连线与I平行。（见图1-1）

A、B表示一排楼房的两个端点，直线I表示公路，很自然地会想到，作线段AB的垂直平分线交I于C点，连接AC和BC，则夹角ACB最大。点C由此而得到。

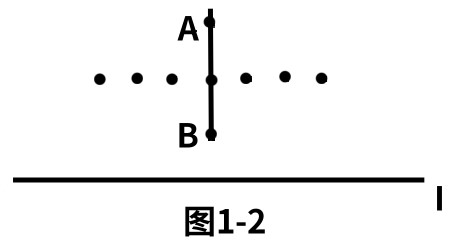
（2）两点的连线与I垂直。（见图1-2)

若还是采用上述方法，由于AB的垂直平分线与I是互相平行的，它们的交点并不存在，所以原有的方法不能采用，下面再看第3种情形。

（3）两点的连线与I斜交。（见图1-3)

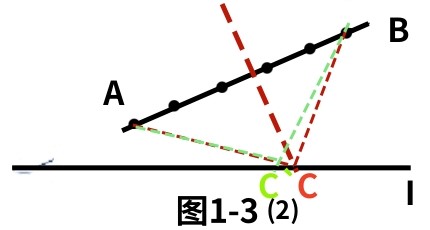
由图1-3（2）可以看到，虽然线段AB的垂直平分线与I的交点C是存在的，但是

角ACB<角AC`B，不是最大的夹角。在上述两种情形中可以看到，利用线段AB的垂直平分线与I的交点C，找最大夹角的方法并不一定是正确的方法，它不适合情形（2）和（3)。那么是否在直线I上一定存在一点X，连接AX,BX，使在这点处有AXB最大？

设想一边沿着直线I走，一边看着线段AB，从直线I与A、B连线的交点出发往右行走（如图1-4)

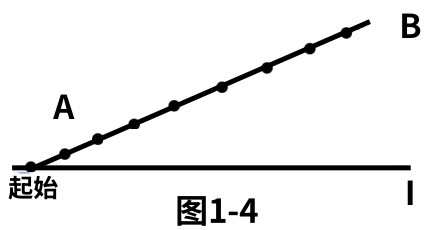
在起点，面对AB的角度为0°，即X从起始位置开始向右缓缓移动，X在起始时的角AXB=0°，而后，角度逐渐增大：到了一定的点后，往后的趋势是当X离起始位置越来越远时，角度再次减少，在无穷远处，角AXB=0。在角度为0的两种极端情形之间。由这样的变化趋势可知，必定在这两者之间取得到最大值。因此一定存在点X，使得角AXB的值最大。

由于直线是向两方无限沿伸，但到底在哪一点可以达到最大值？不妨在直线I上任选一点X，该点是我们随意取的这一点，不一定在我们所要求的最大值的位置上。

如果这一点是最大值的位置，显然已经求得。如果这一点不在最大值的位置上，那么必有另一点，在最大值位置的另一侧，在该点所讨论的角度有相同的值，即是否在直线I上有另外一点X`，使角AX`B=角AXB？

在情形（3）中根据圆的有关圆周角的一个熟知的性质，X与X`（如果X`存在的话）。两点必在通过A、B两点的同一圆周上。于是让我们通过已知点A、B画若干个圆。（如图1-5)

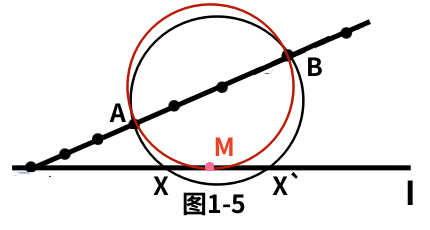
如果这样一个圆与直线I交于两点X与X`,那么同弦所对的圆周角相等，即
角AXB=角AX`B。这个圆中弦XX`上的任意点Y一定有角AYB>角AXB（同弦所对的圆内角大于圆周角）。于是角AXB不是最大的角。只有与直线I相切圆的切点M，才能使观察AB的角度达到最大。（即图1-5中的角AMB).

解：（如图1-6所示）

设经过A、M、B三点的圆的圆心为O，半径为R；过A、X`、X、B的圆的圆心为O`，半径为R`。则O与O`必在AB的垂直平分线上。设AB的中点为C。

因为角AMB、角AXB是圆周角，而角AOB,角AO`B是圆心角，所以

角AMB=1/2角AOB,角AXB=1/2角AO`B

在Rt△ACO和Rt△ACO`中

由于R<R`

由此可得角AMB>角AXB

这是第3种情形下的解题证明过程。

而对于第2种情形同样可以通过此题来证明。但也可推广到用解析几何的解题方法来加以证明。(见图1-7)

以直线I为x轴，A、B的连线为y轴建立直角坐标系。

设A点到x轴的距离（即为到直线I的距离）为a、B点到x轴的距离为b,x即为I
上的任一点，角AXB即为所求的最大的角

设角AXO=a, 角BXO=b，则角AXB=b-a，OX=x

三、 结论

两点在I的同侧，但其位置可能出现三种情形

（1） 两点的连线与I平行：此时最大角在线段AB的垂直平分线交I于C点位置;

（2） 两点的连线与I斜交: 直线I相切圆的切点M，能使观察AB的角度达到最大;

（3） 两点的连线与I垂直: 直线I相切圆的切点M，能使观察AB的角度达到最大,通过解析几何的解题方法来加以证明得出拍照取角

四、 总结

与本课题类似的最值问题还有很多，例如：在足球场上，足球运动员带球射门把门框的两边可以看作是两端点A、B，运动员带球前进所站的位置即为所求的点C，使得角ACB这个射角尽可能大。

生活中存在许多数学问题，我们要善于发现并试图解决

指导老师：刘颖

组长：张欣蕊

组员：丁恒屹，郭嫒霖，权姝文，杜雨轩，梁轩桐，吴欣玥，张莞笛，周雪寒，王琪儿

徐州市第一中学高一（5）班

2024年2月15日